Tato stránka obsahuje nějaká témata, co s pokrýváním plochy nějak souvisí. Není rozhodně úplným výčtem. Naopak se někdy od tématu odchýlí i k nějakým matematicky blízkým záležitostem. Více o laseru, který jsem použil na „vykrajování“ nějakých tvarů najdete na samostatné stránce, kde jsou i odkazy na další vzory, co nesouvisí s tématem.
Stránku jsem rozpracoval, ale pak mi chyběla motivace toho, že by se mi někdo ozval, že to čte. Takže když mi nikdo nenapíše, tak to asi zůstane takhle rozpracované, jak to je…
Pokrývání plochy ne nazývá také teselace (tessellation). Téma, které je jak praktické – popisuje to, jak si můžete například vydláždit koupelnu – tak jde o vědecké téma, přičemž v této oblasti stále probíhá výzkum, jak ukazují objevy z roku 2023. Nebo si prostě můžeme jenom užívat pohled na různé zajímavé vzory. Praktické „vánoční“ využití je při vykrajování z těsta beze zbytků (či s nejmenšími zbytky).
Stránka obsahuje hlavně odkazy na další místa, kde najdete víc. Někde jsou odkazy na soubory pro „tisk“ na gravírovačce, někde na vystřihování, někde moje, častěji cizí (dá se toho najít skutečně hodně již udělaného). Moje soubory různých formátů jsou často nejdřív v balíku zip, protože můj web protestuje při nahrávání nějakých formátů. Budeme se zajímat prakticky jenom o běžnou rovnou Euklidovskou plochu (tedy rovinu či případně papír nalepitelný na stěnu válce; nic co by mělo nenulovou křivost).
Periodické pravidelné vzory
Pravidelné n-úhelníky
Je zajímavostí, že pravidelné n-úhelníky v ploše souvisí s Platónskými tělesy v 3D a dalšími vícerozměrnými pravidelnými útvary, i když pokrývání plochy je spíš samostatný problém.
Úplně nejvíce pravitelné a základní pokrývání plochy je periodické pravidelnými n-úhelníky. Nejmenší počet rovných stran, který může mít rovinný útvar jsou 3. Samozřejmě, že někomu může přijít kružnice jako jednostran, ale kružnice je spíše nekonečně-stran.
3-úhelníky
Rovnostranné trojúhelníky plochu pokryjí s tím, že se pravidelně střídá jejich orientace.
4-úhelníky
Tedy vlastně čtverce. To, že umí pokrývat plochu, je známá věc. V matematice je na tom vlastně založena kartézská soustava souřadnic.
5-úhelníky
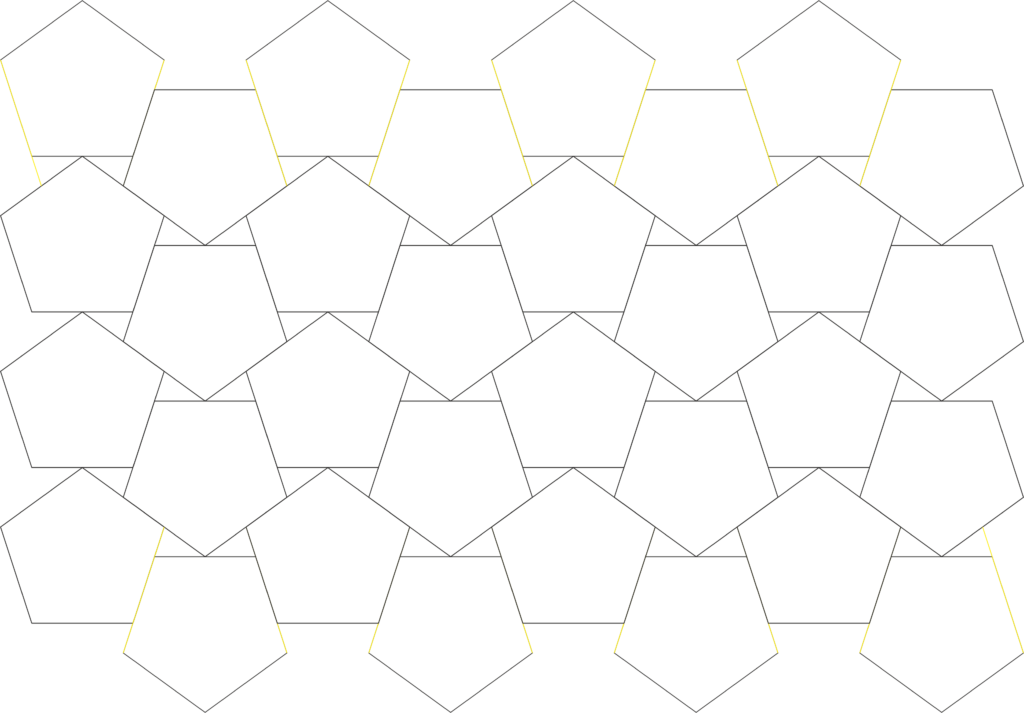
Pětiúhelník nemůže vytvořit pravidelné pokrytí. Místo toho se můžeme snažit na jednotkovou plochu „nacpat“ co nejvíce pětiúhelníků. Zdá se, že by mělo jít o toto uspořádání, kde jsou kombinované s trojúhelníky. Nicméně jde pouze o článek v preprintu, který ještě nebyl oficiálně vydaný, takže důkaz má asi nějaké mezery. Určitě jde ale o jedno z nejtěsnějších uspořádání a docela pravděpodobně to nejkompaktnější.
Při vyřezávání na ploše s tímto úsporným uspořádáním nám tedy zbudou ještě malé trojúhelníčky.
Pětiúhelníky v souboru Corelu, v SVG a v Lightburn. Jsou tam nějaké žluté vodicí čáry – to mi pomáhalo pro správné umístění v Corelu tak, abych se skutečně trefil s tím nejtěsnějším uspořádáním a nepřekrývalo se to.
6-úhelníky
Šestiúhelníky pokrývají plochu typicky známým třeba z úlů včel, kde většina buněk má právě pravidelný šestiúhelníkový tvar. Přičemž to není nějaká náhoda, ale kompromis mezi tím, že kruh má největší objem na co nejméně materiálu. Ale na druhou stranu chtějí včely mít co nejvíce buněk na co nejmenší ploše, takže se musí všechny dotýkat. Proto vznikne právě šestiúhelníkové pokrytí.
Z trojúhelníkového pokrytí snadno dostáváme šestiúhelníkové a naopak.
>= 7-úhelníky
Pro více jak pravidelné šestiúhelníky už se nám nepodaří plochu pokrýt beze zbytku. Můžeme se ji snažit případně pokrýt kombinacemi různých geometrických tvarů. Nebo hledat nejkompaktnější pokrytí. To je pravděpodobně např. u sedmiúhelníku obdobné tomu, co u pětiúhelníku.
Ne tak pravidelné n-úhelníky

Pokud snížíme požadavky na to, že sice chceme n-úhelník, ale nevadí nám, že bude nepravidelný nebo dokonce nebude třeba ani konvexní, tak se nám otevírá první širší skupina pokrytí plochy.
Snadno pokryjeme plochu různými trojúhelníky, čtyřúhelníky a šestiúhelníky. Dále pak útvary, které mohou vzniknout například jejich rozdělením a tu přidáním a jinde odebráním kousku dílku.
Například již existují pětiúhelníky, které pokryjí celou plochu.
Dílky pokrývající plochu stejně pravidelně jako pravidelné n-úhelníky, ale s daleko komplikovanějším vzorem
Podobně jako v předchozím kroku jsme snížili pravidelnost, tak můžeme vyjít z trojúhelníkového, čtvercového nebo šestiúhelníkového pokrytí plochy, využít jejich symetrii, pohrát si s okrajem a dostaneme nějakou pěknou věc pro pokrytí.

Třeba jde o ještěrky (plazy, reptile, salamandry… co si pod tím představíte) od E. C. Eschera, kterými můžeme pokrýt plochu. Ty i pěkně po poskládání za sebe drží svými nožičkami a ocásky. S tím, že jsou jinak prakticky ekvivalentní pokrytí plochy trojúhelníky.
- Ještěrky na stříhání v PDF.
- Odkaz na původní zdroj či alternativní zdroj.
- Na 3axis.co je podklad pro řezání v kruhu (já jsem si ale upravil ty předchozí na relativně velké využití A4).
- Ukázka nepraktického ne-pokrývání plochy je taky na 3axis.co.
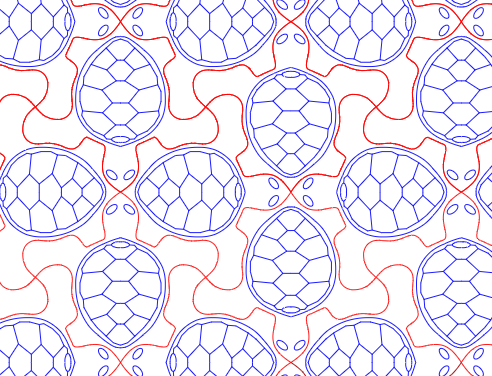
Dále pak jsou třeba pěkný tvar želvičky, které jsou ekvivalentní pokrytí čtverci (či možná spíš kosočtverci či čtverci a otočením sítě). Na ukázce vedle vidíte dvě barvy, což je právě příprava pro tisk na gravírovačce, kde jednou barvou jsou věci, které se jenom „vyryjí“ (zde modrá) a jinou barvou, co se vyřízne (zde červená).
Čím plochu nepokryjeme
Otázka pokrytí plochy souvisí s tím, že jsou dílky, kterými plochu nepokryjeme, ať se budeme, jak se budeme snažit. Respektive se můžeme snažit opakovat nějaký tvar menší a menší tím plochu pokrýt. Nebo vzít kombinaci tvaru a toho, co nám potom, co ho vyřízneme co nejblíže u sebe, zbývá a to prohlásit za kombinaci dvou či více dílků, které využijeme.
Kruhy
Nejpravidelnější rovinný útvar je kruh. Ale, jak je možné se snadno přesvědčit, tak není možné kruhy pokrýt plochu. Respektive, mohli bychom definovat nějaký rekurzivní/fraktální postup, jak umisťovat čím dál tím menší kruhy. Ale s kruhy nejde pokrýt plochu, pokud máme definovanou velikost, resp. ani s jakoukoliv konečnou kombinací kruhů s konečně velkými rozměry.
Fordovy kruhy
S pokrýváním plochy souvisí jenom částečně – jde vlastně o konstrukci, ve které vytvoříme nejdřív kružnici nad 0 a 1 nad číselnou osou a pak doplňujeme vždy největší kružnice. Docela zajímavé je, že čísla, ze kterých postupně kružnice tvoříme, dostáváme „špatným sčítáním zlomků“ (Fareyho sčítání, posloupnost), kde se vždy u sousedních čísel sečtou čitatelé a jmenovalé a vznikne nový zlomek. Tedy když začínáme od 0 a 1, dostáváme některé první členy
\(\displaystyle \frac{0}{1} \oplus \frac{1}{1} = \frac{1}{2} \, ; \quad \frac{0}{1} \oplus \frac{1}{2} = \frac{1}{3} \, , \quad \frac{1}{2} \oplus \frac{1}{1} = \frac{2}{3} \, ; \quad \frac{1}{2} \oplus \frac{2}{3} = \frac{3}{5} \, \dots \)
Pokud budeme pokračovat do nekonečna, tak pokryjeme všechna racionální čísla na číselné ose od 0 do 1. Ale nezasáhneme ani jedno iracionální číslo na ose. A vyplnění prostoru nad osou bude také značně „děravé“.
Heeschovo číslo (Heesch number)

druhou koronu se vám už nepodaří vytvořit
Heeschovo číslo pro nějaký dílek udává počet „korón“ či „obalů“, které jde vytvořit opakováním stejného dílku. Pěkně vysvětlené je to na anglickém webu. Pokud je dílek např. kružnice, tak je tento počet 0, protože nevytvoříme ani jeden obal. Pokud si vybereme čtverec, tak korón můžeme vytvořit neomezeně mnoho a tak je Heeschovo číslo \(+ \infty\). Tedy mít dílek, který pokryje plochu, je ekvivalentní tomu, že Heeschovo číslo je \(+ \infty \). Existují i různé příklady dílků, u kterých jde vytvořit 1, 2, 3, 4, 5 či 6 (poslední objeveno v 2020). V současnosti je domněnka, že by mohly existovat dílky pro každé přirozené Heeschovo číslo, ale není jasné, jestli to nebude časem vyvráceno, je to nedokazatelné, nebo je to jenom velice těžké dokázat. Také tvary pro velká čísla (a současně menší než nekonečno), které se zatím objevily jsou dost komplikované.
Další ukázky dílků a jejich korón jsou na dalších stránkách stejného webu.
Fraktální vzory
Fraktály nejsou úplně praktické, co se týče přesně fyzické realizace, ale je možné se k nim alespoň přiblížit.
Fraktální okraje
- Dračí křivka – její postupné iterace se dají skládat z papíru, resp. ty první
- Kolakoski-(3,1), with dual – je to zajímavé tím, že ty okraje vypadají hodně zvrásněně a že by to nemělo sedět, ale když se to vyřeže ve správném poměru, tak to zapadá fakt dobře a i podle té konstrukce na stránce je vidět, jak se dají skládáním zkonstruovat větší dílky, které jsou podobné těm původním – soubory pro Lightburn (malinké a větší ve vhodném měřítku)
Fraktály zaplňující plochu
Mezi fraktály jsou vzory, které nějakým způsobem zaplní celou plochu (či N-dimenzionální prostor). Příkladem může být
- Hilbertova křivka – vzniká postupným nahrazováním svých „podčástí“ za „více zvlněné“ a tím po nekonečném počtu iterací dokonale pokryje celou plochu. Tedy i když pokryjeme konečný čtvereček, tak je její délka nekonečná. Ale to je přirozené, když s křivkou chceme pokrýt plochu.
Fraktály, co nepokryjí plochu, ale mají pěkný vzor
- Sierpinského trojúhelník – naopak od Hilbertovy křivky, kde z křivky vzniká plocha, tak Sierpinského trojúhelník můžeme konstruovat odstraňováním vnitřní čtvrtiny trojúhelníku a to až tak, že dostaneme takový útvar, kde při náhodném výběru bodu se souřadnicemi uvnitř původního trojúhelníku máme pravděpodobnost, že trefíme mimo, rovnou jistotě – jeden trojúhelník svg, několik trojúhelníku lbrn2
Aperiodické pokrývání plochy
Aby bylo pokrytí plochy trochu zajímavější než jenom periodické, tak jsou taková pokrytí, která jsou aperiodická a to i když používáme stejnou sadu dílků či dílek. Nejdříve se objevovala postupně taková pokrytí, která využívala mnoho různých dílků. Později počet klesal. V roce 2023 byl objeven takový dílek, kterým můžeme, při vhodném pokládání, aperiodicky pokrýt celou plochu.
Proč při vhodném pokládání? Protože pokud nedodržujeme nějaká pravidla, tak u některých dílků můžeme dospět k pravidelnému pokrytí. Nebo v nějakých případech, kdy nám sice třeba ani dílky nedovolí tato pravidla nedodržet, tak můžeme dojít k tomu, že jsme je poskládali tak, že se nám do nějakého místa už nedá umístit žádný další dílek (což by se dalo ověřit i na nějakém z dalších materiálů, které tu uvidíte).
Aperiodická pokrytí souvisí ve fyzice s kvazikrystaly.
Penroseovo pokrytí
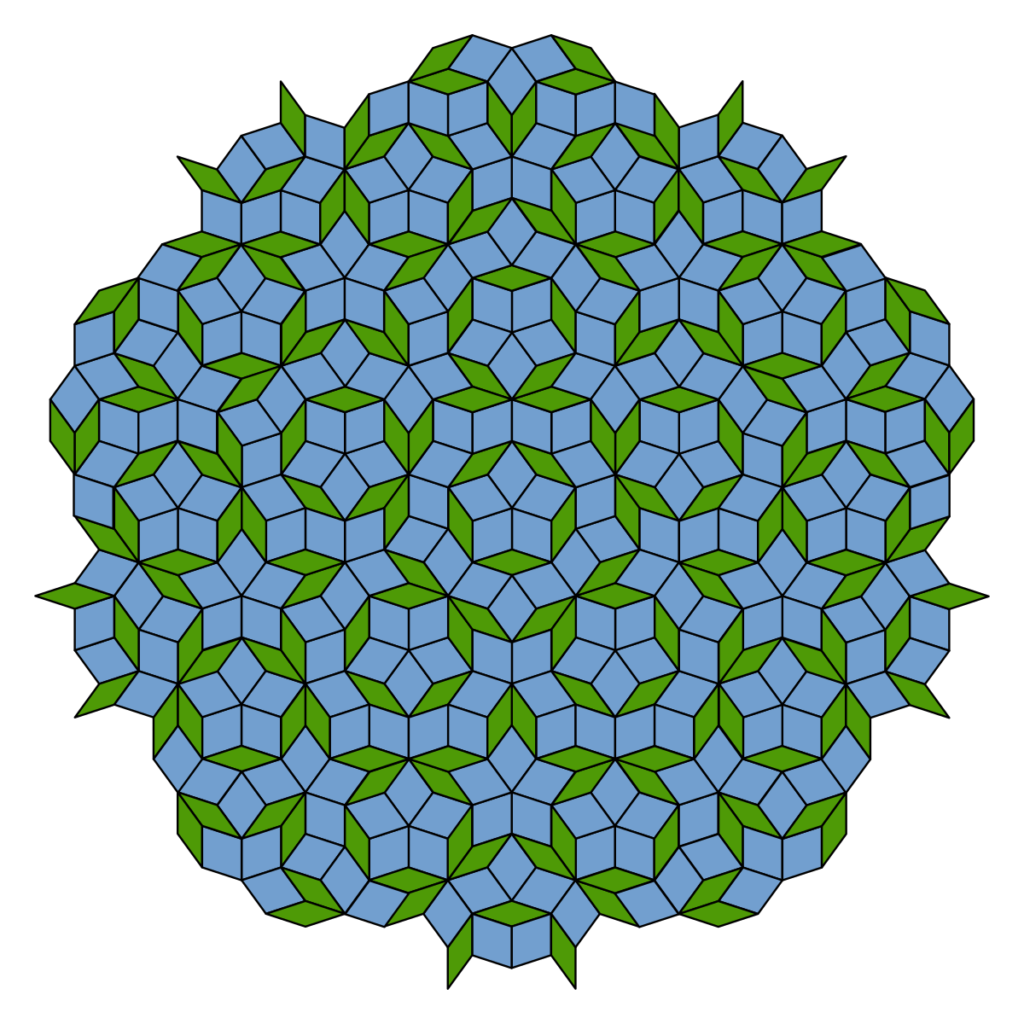
Penrose byl první, komu se podařilo vytvořit podle nějakých pravidel nepravidelné pokrytí za použití pouze malého počtu dílků (předtím byla známá taková, která pokrývala plochu s hodně velkým počtem dílků), a hlavně se jako první dostal na 2. Existuje více druhů pokrytí, na které přišel a které pokrývají plochu aperiodicky.
Aperiodic monotile
Objev z roku 2023. Nejprve se objevil díle, kterým jde aperiodicky pokrýt plochu, když ho otáčíte (respektive dva tvary, které se nazvaly hat = klobouk a turtle = želva). Prakticky hned po publikaci prvního článku se pak objevil ještě další tvar, který dokáže pokrýt svým opakováním plochu bez otáčení.
- Stránky autorů článku o objevu.
- Podklad na A4 ke stříhání (spectre). /A ano, tohle má zrovna tolik oblých rohů na stříhání, že je to docela náročné./


